The basic mechanismes for the particle propagation are:

The ether cubes in the centre row - where the particle can be located - turn by 90 degrees each, while the particle passes. This 90 degree turn (or a mutitude of 90 degrees) is essential for the existance of the cavity within the ether. So even, when the particle is slow or even at rest, the cubes will hold the cavity open; it cannot collapse by the external pressure, als long as the cubes maintain their size.

analogy to turned cards.

This particularity has a good analogy in a card deck. As the picture shows, the cards may be shown with the front face or the back simultaneoulsly. But there is a distortion in the centre, where the cards are standing upright. This distortion stays for the cavity in the ether, which will in any case be hold open, even when the particle is at rest.

So, the model states that elementary particles are cavities within the ether. The ether - here represented by the cubes - shows cracks with about even spacing of an elementary length. The elementary particle has an energy, which stands for the volume of the cavity. The particle spin is responsible for the turns of the cubes. The (de Broglie) wave length of the particle stands for the length of the disturbance, the particle imposes on the ether.

The model can visualise one important fact in modern physics, which hitherto could not be modelled satisfactorily: the appearent size of elementary particles (e.g. its wave length, which for most particles stands for the volume occupation) increases as the energy becomes smaller. This model may explain that the particle wave length shortens as the energy (=volume) increases, thus allowing for the cubes to turn much quicker.

Different particle species differ with respect to the disturbance in the ether. Furthermore, the ether cubes can fraction easily, whereby the fractions are also - due to the mechanismes of fractioning - essentially rectangular.

The whole physics - according to this model - boils down to geometric effects. The material properties of the ether are not complex.

The elementary particle shown in the animated picture may stand for the light quantum. I think, however, that the ether cubes deteriorate a little bit as the quantum passes. Thereby, the ether cubes form a powder, which fills the gaps at the righ hand side of the animated picture. This pulverisation does imply that the time "axis" cannot be reversed.

cavity and ether cubes.

This fractioning of the ether is shown in the above picture. Here again, the particle (cavity) moves from right to left. As the cavity "intrudes" the ether and twists the cubes, the cubes are reduced in size, because the forces on the edges cause the ether cubes to wear off. The "dust" is essentially cubic as well. So, when the debris is compresses at the right hand side of the picture, all ether particles gain a rectangular alignement with the surfaces beeing essentially parallel to the original position. The important difference is, that the main parts of the original cubes have been turned by 90 degrees.

The "dust"- particles of the ether may be very fine. There is no indication as to a sort of minimum size. On the other hand, all dust particles have in common that they are of rectangular shape. Therefore, as the dust compresses on the right side in the picture, it forces the upstream cubes to turn.

Due to the external pressures, the dust particles can move within the cavities with a maximum speed, which is known to us as the "speed of light". There is, however, an even larger speed. This is the speed of crack formation within the ether. According to the model, the cracks may propagate with "infinite" velocities. But any newly formed crack will close instantly, unless it is filled with "ether powder". Therefore the speed of propagation of any particle (cavity) is limited to the speed of the ether dust as it partially fills the cracks and thereby opens the cavities in the forefield of the particle.

The external pressure is not static. Instead, the pressure pulses with a periodicy of 10E-23 sec.

So, with the maximum speed of the ether dust being equal to the "speed of light", the periodicity of the pressure leads to a periodicity of the cracks in the ether. This determines the size of the cubes to roughly as 10E-15 m, or as the "elementary length".

As long as the powder remains rectangular, the total volume of the the cavity is basically independent of the grain size. This is an important fact when one consideres, how the volume of the cavity is influenced by the decay of the ether cubes. The important thing is that the fine powder cubes are still parallel, when they are compressed.

The picture can also visualise the correspondance between the vortex cristal model and the ether model. The cavity is distributed between many cubes. Every open space is surrounded by a moving medium, which has a vorticity around all open spaces. These open spaces correspond to the vortex rings, which - as the vortex crystal model stated - are aligned along an axis.

vortex crystal model.

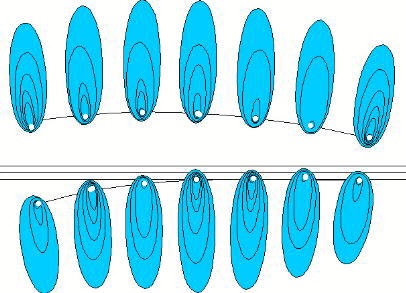Previous to the ether model, my analysis concentrated on the vortex crystal model. Thereby the elementary particles were asumed to be alignements of vortex rings. These are aligned along the axis of propagation. The spacing of the vortex rings being the elementary length.

The picture shows a cross section of a vortex crystal system. The blue parts in the picture represent the eddies of the vortex rings. Basically, the whole space is filled with a fluid. But the smallest circles (white dots in the blue areas) are the cross sections of the evacuated rings.

In total, the volume of all cavities within the vortex rings sums up to a constant value. The vortex crystal is basically as long as the de Broglie wave length.

When the particle moves slowly, (thus the wave length being large) its volume is distrubuted over many vortex rings. Each individual ring has only a small ring cavity. If, however, the speed is large, there are only a few vortex rings, each having a rather large cavity volume.

There is a steady flow along the axis. The model suggests, that one of the rings is tracked into the axial flow, thereby the vortex ring is stretched to the total length of the crystal. This was considered the mechanisme, which keeps the whole assembly together.

Numerical evaluations can show that thereby the kinetic energy corresponds to a fraction of this elongated ring, which just amounts to half of spacing of the vortex crystal.

This exemple shows that the vortex crystal model has particular advantages: it reduces terms as total energy content, kinetic energy, spin etc. to a mainly geometrical system within three space dimensions. My calculations even lead to very simple correspondences of natural constants, which all were interrelated by "powers of pi".

The two models shown here are two sides of the same face. The models have in common to attribute elementary particles to cavities within the ether.

Short term effects can be modelled using the ether cube view. Slow particles with long wave length might better be modelled using the vortex crystal view. This may be due to the steady fractioning of the ether, as long as the particle passes. Thereby the ether will essentially behave like a fluid rather than a pile of bricks.

extended vortex crystal model including ether bricks.

This is shown in the above picture, which includes the vortex rings and the ether bricks. Thereby the ether bricks have typical dimensions of an elementary length; the cubes are generated by the universal pulse, which tics like a gigantic clock and thereby imposes periodic pressures on all places. This periodicity is transfered to a periodic pattern in space.

This model allows for a large variety of "particle particularities", whereby electric charge, mass, inertia etc. may find an analogon in geometric terms. The model may prove Descartes right, when he postulated that all material properties, all physics, are of geometric origin.

The vortex crystal model, however, did not provide for an easy way to explain, why the vortices are spaced by the elementary length, and that the radius of the evacuated rings should also be an elementary length.

This was easily explained in the ether cube model. Thereby the vortex crystal model had to be extended insofar, as there there are many concentric rings, in one cross section, each being separated from the others by an elementary length; as the ring diameter increases, the volume of the evacuated ring and the vorticity decreased.

Furthermore, this model also explaines, why quantum mechanical equations have so much in commen with viscous flows (or shear flow): As the cubes turn and twist, all movements along the axis of propagation lead to an ether movement along the other spaces coordinates.

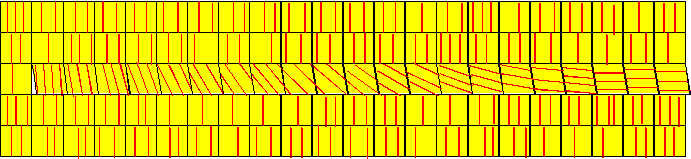Modelling a light quantum.

This pictue shows a slightly different view to the ether model. Thereby it is asumed that the ether cubes in the centre row are rearranging with the ether powder, thereby getting a rhombic shape.

The light quantum cavity is represented by the small triangle in the centre row. This volume stands for the energy of the quantum. As smaller the volume, the smaller the energy. All subsequent cubes (to the right) are deformed a bit. The orientation of the original ether material is shown by the red lines. So, all the cubes "downstream" of the cavity continue turning, unless they reach an tilt angle of 90 degrees. But, at every pulse, the cubes are reshaped.

By this view, one might take into account that all cubes are partially pulverized, where the powder still has rectangular shapes and thereby forces the ether "bricks" to align according to the previous position. The powder may instantly - within a few universal pulses - attach to the cubes, even before they have completed their turning. It is essential, however, that the ether material itself is considered incompressible; this means, it can bear any physical pressure without being compressed; all compressions take place within the cavities in the ether.

This picture can explain, why the wave length of light is as larger as smaller the energy is. At every pulse of the universal clock, the cavity moves one elementary unit length to the left, e.g. the length of one cube. All subsequent cubes are turned by the small angle of the triangle. Since the "angular velocity" of the turning motion is directly related to the angle of the triangle, the total "spin" (momentum of angular motion) is independent of the energy, whereas the energy of the angular motion is directly proportional to the volume of the triangular cavity (this is a very easy calculation). Thus the model may serve to eventually understand, why spins of particles are independent of energy and momenta.

It is seen as one of the virtues of the ether model to visualise the quantum mechanical quantities like "spin", wave length, and others in simple mechanical terms.

It also allows to visualise, why there are some particles (as light quanta), which can migrate through the space without being disturbed by other particles, whereas other particles (as electrons) obey the Pauli principle, thereby excuding other particles of the same quantum state to share the same volume (within the wave length).

Time seemed ripe for abandoning the ether theory 100 years ago. In my believe, Micheslsonīs experiment was not so essential at all for the ending of the ether theory. What scientists dit not like was the previous finding, which proved that light is a transversal wave rather than a longitudinal wave. Scientist had problems in finding any model at all for showing, what sort of ether property might be responsible for the "vabrations" to take place pependicularly to the direction of the light ray.

The same problem, still, does apply for the electric and magnetic field forces. And this question is not solved by modern science: the attribution of virtual light quanta to electric and magnetic fields does only shift the problem to a higher level.

One thing, which can satisfactorily be explained by the ether model is the nature of virtual particles: As the ether cubes have to turn by a multitude of 90 degrees to stay stable, the same sort of ether motion can happen, whereby the turn is less than 45 degrees. Thereby the cube returne to their original orientation and eventually the cavity collapses. Thus, this sort of elementary particle is not real, but it exists - as modern physics postulates for a time span, which is in line with the uncertainty relation; and the short term particle is able to transfer forces and energy: these are the "virtual" particles, which are the basic building bricks of quantum electrodynamics.

As the ether model shows, these virtual particles may exist in complete agreement with quantum field theory.

Letīs fight for the end of the irrational age!

Sometimes there are periodic clouds in the summer sky. They seem like being brushed onto the sky by a giant feather. This sort of cloud formation cannot be explained satisfactorily by modern meteorology. I think, this phenomenon does directly reveal the cracks in the ether, the earth meets, as the solar system moves through the galaxy. I consider these feather clouds as one of the direct proofs for the ether model.

Modern science has developed a special way of saying things. One particularly interesting phrase is: "...due to reasons, which are not yet fully understood".
In plain words this phrase means: "We have not the slightest idea, how this phenomenon might be explained. All attempts in solving the problem have failed."
There are many things in modern science, "which are not fully understood"; e.g. the sun spots, the phenomena of turbulence, the fact that the solar corona is hotter than the photosphere, and many more.
I believe that many of these phenomena may eventually be understood on the ground of the ether model.

If You like more more information in german , please click here.

If You like to return to the english page, please click here.

date of last issue: 14. 4. 1997